
Connecting pre-university students with professional science
Contextual Curriculum Connections
A6 Falling under gravity in non-resistive and resistive media
in the context of atmospheric monitoring with weather balloons
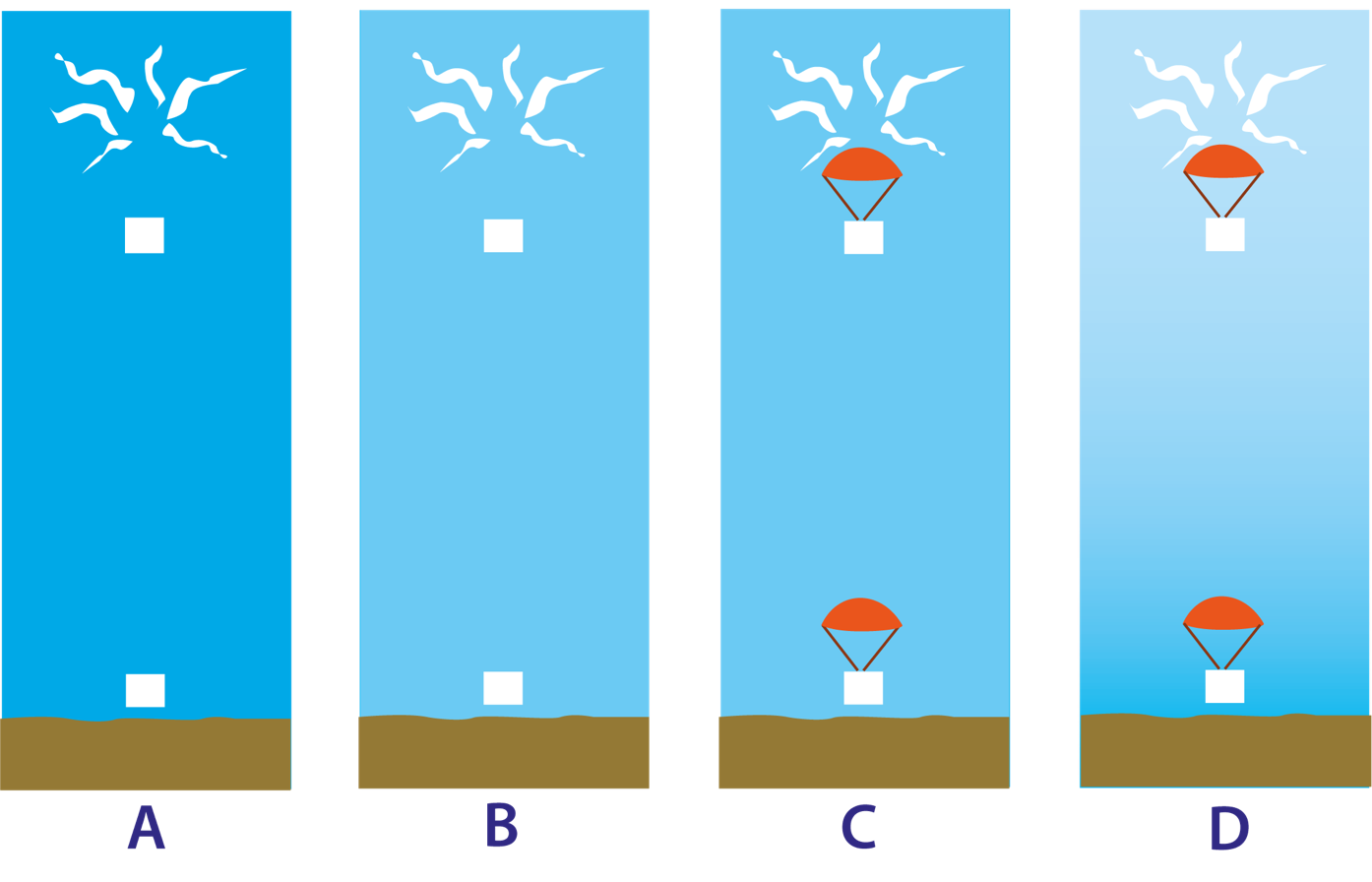
Ascent, burst, and parachute descent of a weather balloon in the USA. (Also featured in topic A7.)

Weather balloons carry sensing devices that then send their measurements of pressure, temperature and humidity back to the weather station. These devices are radiosondes.
balloon bursts at ‘initial altitude’ of 33 km
ground level altitude 0 km
radiosonde falls, without parachute
radiosonde falls, without parachute
radiosonde falls, with parachute
radiosonde falls, with parachute
No resistance
With resistance
With resistance
With varying density of the air
Radiosonde: equipment for atmospheric measurement with a radio transmitter to send the data to a ground station.
The image shows four scenarios. Since it can be useful to begin with a simple case, A shows a radiosonde falling without a parachute through a non-resistive medium. The simplest scenario here can be called an ‘ideal’ case.
In B and C, there is air resistance. In D, the atmosphere has varying density and so the air resistance increases during the fall. D is the most realistic representation.

Scenario A, fall from rest with uniform acceleration through a non-resistive medium with fixed density
acceleration, a = (v - u) / t
at = v - u
v = u + at
average speed = s / t = (v + u) / 2
2s = (v + u) t
Since v = u + at,
2s = (u + at + u) t
= 2ut + at2
s = ut + 1/2 at2
It’s possible to combine these two equations to eliminate t:
v = u + at
So
t = (v - u) / a
s = ut + 1/2 at2
s = u (v - u) / a + 1/2 a (v - u)2 / a2
s = (uv - u2) / a + 1/2 (v - u)2 / a
as = uv - u2 + 1/2 (v2 - 2uv + u2)
as = -u2 + 1/2 v2 + 1/2u2
as = 1/2 v2 - 1/2u2
2as = v2 - u2
v2 = u2 + 2as
The highlighted equations are three ‘equations of uniformly accelerated motion’.
Selecting the equation to match the available information:
v = u + at
s = ut + 1/2 at2
v2 = u2 + 2as
useful for finding v, u, a or t without needing to know s (distance)
useful for finding s, u, t or a without needing to know v (final velocity)
useful for finding v, u, a or s without needing to know t (time)

Scenario B, fall from rest with uniform acceleration through a resistive medium with fixed density
Until the balloon bursts the load is moving upwards. It then accelerates downward due to gravity.
The load’s velocity soon reverses in direction and increases, downwards. As velocity increases, so does the upwards force due to the air resistance.
The resistive force keeps increasing as long as velocity keeps increasing. The upwards resistive force becomes as big as the downwards gravitational force.
There is then zero net force. So there is now zero acceleration. That means there must be constant velocity. It’s called the terminal velocity of the fall.
The load continues falling at this velocity until it reaches the ground.
For most falling loads the terminal velocity is too high to prevent damage on contact with the ground – in the impact there is a large upwards force.

Scenario C, increasing the rate of increase of the resistive force, to reduce terminal velocity
Use of a parachute allows resistive force to become the same size as the gravitational force more quickly.
Terminal velocity is greatly reduced, and now the load can survive impact with the ground.

Scenario D, the density of the medium can increase during the fall
In a non-uniform medium, such as the atmosphere when falling from 33 km, to predict the load’s velocities it’s necessary to take the varying density of the medium into account.
That complicates the maths, but it’s still possible. Fortunately, it’s not something to worry about just yet.
Environmental concerns about weather balloon debris.
(C) David Brodie 2025 Note that all external videos and websites remain copyright of the creators
